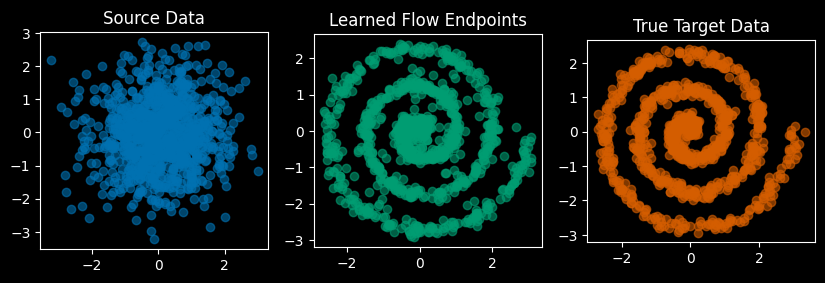
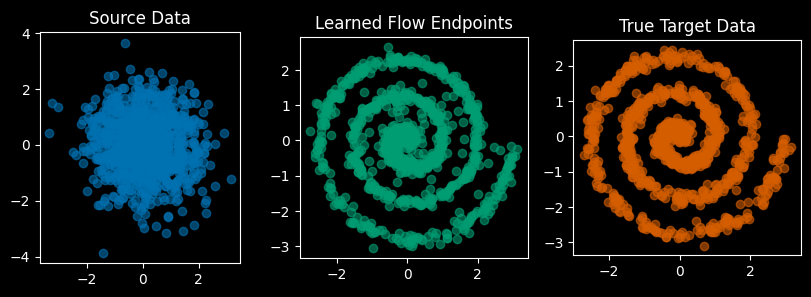
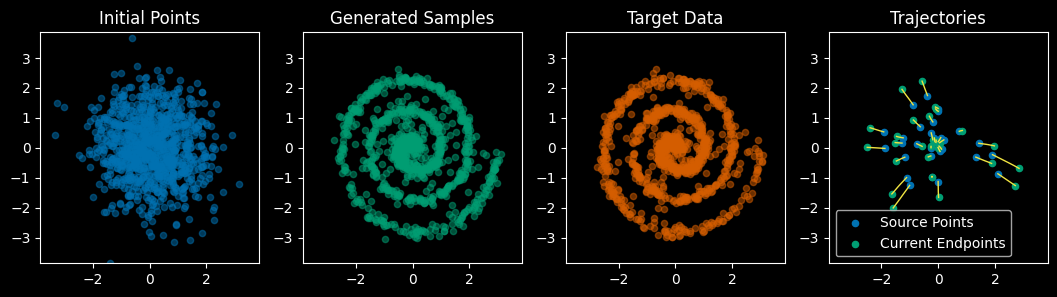
@torch.no_grad()
def create_streamline_animation(start_dist, model, model2=None, n_frames=50, show_points=False, titles=None,
step_fn=fwd_euler_step, # euler's ok for reflowed model bc/paths are straight
save_file=None,
):
"""Create an animation showing distribution flow with streamplot background"""
device = next(model.parameters()).device
figsize = [5,5]
if titles is None:
titles = ['Flow Matching']
if model2: titles += ['Reflowed Model']
if model2:
figsize[0] *= 2
n_plots = 1 + (model2 is not None)
fig, ax = plt.subplots(1, n_plots, figsize=figsize)
if n_plots==1: ax = [ax]
plt.close()
end_dist, trajectories = integrate_path(model, start_dist.clone().to(device), n_steps=n_frames, step_fn=step_fn, warp_fn=warp_time, save_trajectories=True)
scatter = ax[0].scatter([], [], alpha=0.6, s=10, color=wong_pink, zorder=1)
if model2:
_, trajectories2 = integrate_path(model2, start_dist.clone().to(device), n_steps=n_frames, step_fn=step_fn, warp_fn=warp_time, save_trajectories=True)
scatter2 = ax[1].scatter([], [], alpha=0.6, s=10, color=wong_pink, zorder=1)
max_range = max( abs(start_dist).max().item(), abs(end_dist).max().item() )
for i in range(len(ax)):
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
ax[i].set_aspect('equal')
if titles: ax[i].set_title(titles[i])
# Create grid for streamplot
grid_dim = 50
x = np.linspace(-max_range, max_range, grid_dim)
y = np.linspace(-max_range, max_range, grid_dim)
X, Y = np.meshgrid(x, y)
# Convert grid to torch tensor for model input
grid_points = torch.tensor(np.stack([X.flatten(), Y.flatten()], axis=1), dtype=torch.float32).to(device)
color = wong_pink if show_points else (0,0,0,0)
dt = 1.0 / n_frames
def init():
for i in range(len(ax)):
ax[i].clear()
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
scatter.set_offsets(np.c_[[], []])
if model2:
scatter.set_offsets(np.c_[[], []])
return (scatter,scatter2)
return (scatter,)
def animate(frame):
for i in range(len(ax)):
ax[i].clear()
ax[i].set_xlim((-max_range, max_range))
ax[i].set_ylim((-max_range, max_range))
if titles: ax[i].set_title(titles[i])
ax[i].set_xticks([])
ax[i].set_yticks([])
for spine in ['top','right','bottom','left']:
ax[i].spines[spine].set_visible(False)
# Update scatter plot
current = trajectories[frame]
scatter = ax[0].scatter(current[:, 0], current[:, 1], alpha=0.6, s=10, color=color, zorder=1)
if model2:
current2 = trajectories2[frame]
scatter2 = ax[i].scatter(current2[:, 0], current2[:, 1], alpha=0.6, s=10, color=color, zorder=1)
# Calculate vector field for current time
t = torch.ones(grid_points.size(0), 1) * (frame * dt)
t = warp_time(t).to(device)
velocities = model(grid_points, t).cpu()
U = velocities[:, 0].reshape(X.shape)
V = velocities[:, 1].reshape(X.shape)
x_points = np.linspace(-max_range, max_range, 15)
y_points = np.linspace(-max_range, max_range, 15)
X_arrows, Y_arrows = np.meshgrid(x_points, y_points)
start_points = np.column_stack((X_arrows.ravel(), Y_arrows.ravel()))
ax[0].streamplot(X, Y, U.numpy(), V.numpy(),
density=5, # Controls line spacing
color=line_color, # (0, 0, 1, 0.7),
linewidth=0.8, maxlength=0.12,
start_points=start_points, # This should give more arrows along paths
arrowsize=1.2,
arrowstyle='->')
if model2:
velocities2 = model2(grid_points, t).cpu()
U2 = velocities2[:, 0].reshape(X.shape)
V2 = velocities2[:, 1].reshape(X.shape)
start_points2 = np.column_stack((X_arrows.ravel(), Y_arrows.ravel()))
ax[1].streamplot(X, Y, U2.numpy(), V2.numpy(),
density=5, # Controls line spacing
color=line_color, # (0, 0, 1, 0.7),
linewidth=0.8, maxlength=0.12,
start_points=start_points2, # This should give more arrows along paths
arrowsize=1.2,
arrowstyle='->')
# Update particle positions
t = torch.ones(current.size(0), 1) * (frame * dt)
t, dtw = warp_time(t, dt=dt)
velocity = model(current.to(device), t.to(device)).cpu()
current = current + velocity * dtw
if model2:
velocity2 = model2(current2.to(device), t.to(device)).cpu()
current2 = current2 + velocity2 * dtw
return (scatter, scatter2,)
return (scatter,)
anim = animation.FuncAnimation(fig, animate, init_func=init,
frames=n_frames, interval=20, blit=False)
if save_file:
anim.save(save_file, writer='ffmpeg', fps=30)
return HTML(f"""<center><video height="350" controls loop><source src="{save_file}" type="video/mp4">
Your browser does not support the video tag.</video></center>""")
else:
rc('animation', html='jshtml')
return HTML(anim.to_jshtml())
save_file = 'images/fm_vs_rf_streamvecs.mp4'
create_streamline_animation(val_points, fm_model, model2=reflowed_model, n_frames=50, save_file=save_file)#, show_points=True)





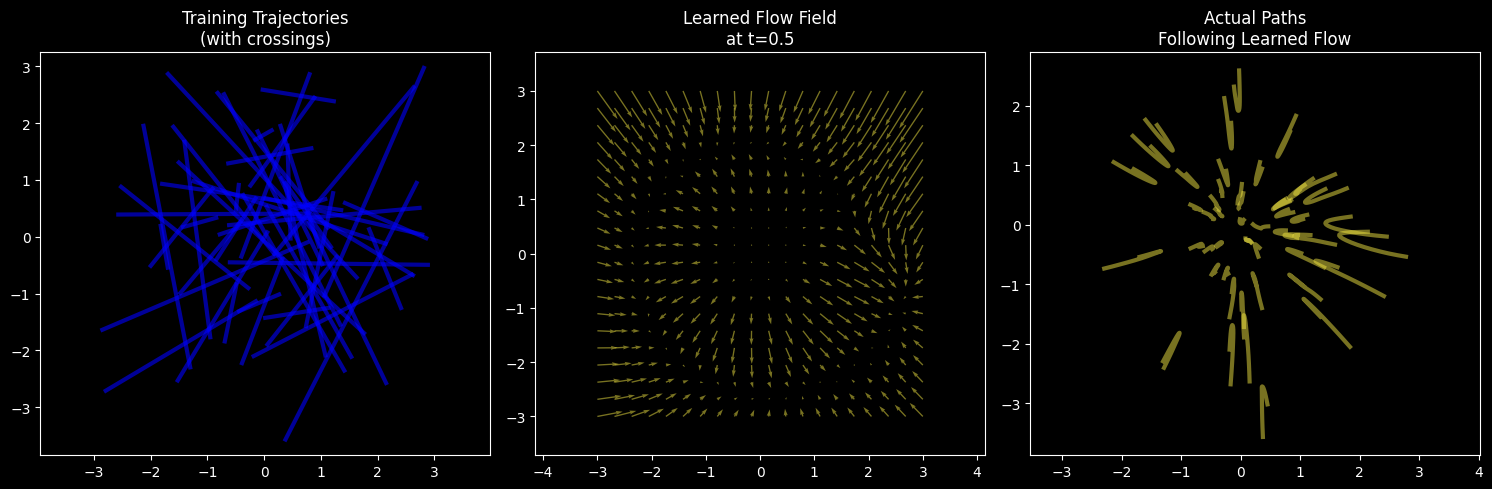
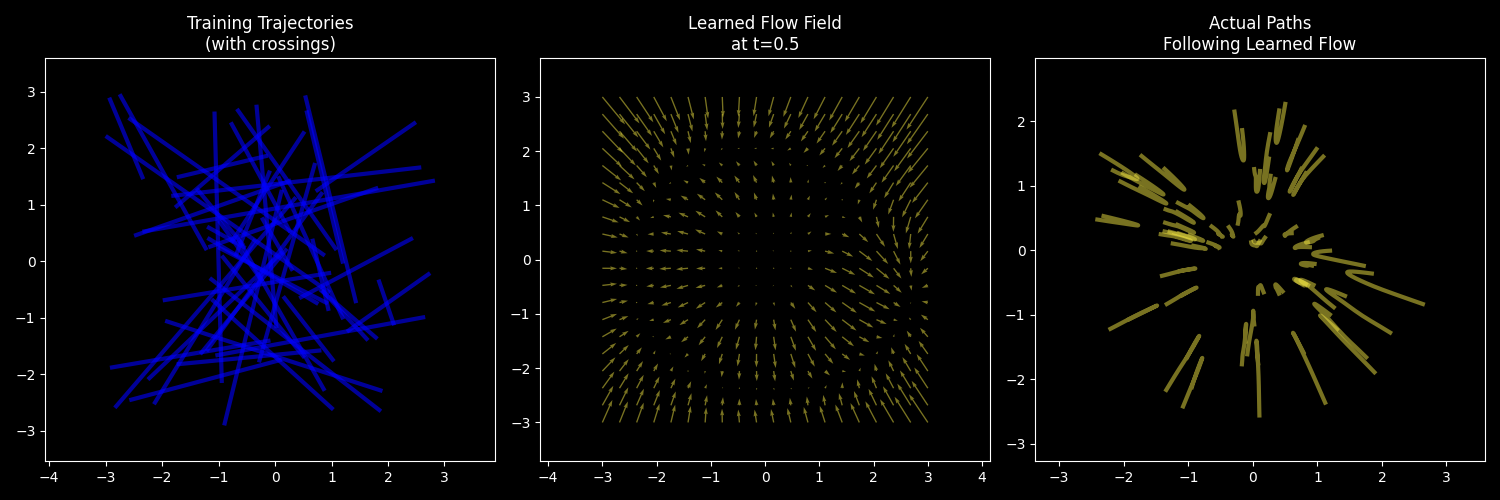 Left: Training data uses simple straight lines (with many crossings). Middle: The learned flow (velocity vector) field is smooth and continuous. Right: Actual trajectories following the flow field don’t cross.
Left: Training data uses simple straight lines (with many crossings). Middle: The learned flow (velocity vector) field is smooth and continuous. Right: Actual trajectories following the flow field don’t cross.