blog - Learning Room Shapes (with Neural Networks)

‘Deep’ neural network learns (boxy) room shape given mode frequencies, or vice versa.

This is just a quick note, sharing a new “toy” result, that relates to function spaces, acoustics, and machine learning. I never bothered to publish it, because I was just “playing around”. The real trick would be to extend this to “non-boxy” room shapes, which…turns out to be hard! haha

Main Python code for this is here.

Motivation

During Karlheinz Brandenburg’s visit, he remarked that learning room shapes from the sound of the room is still an open question. So yesterday, “for fun” I decided to try the easiest possible thing I could think of, the most “ideal” if you will: wrote a NN system that learns to use a set of room mode frequencies to predict (boxy) room dimensions, or vice versa, i.e. it learns the “Rayleigh Equation” for 3D standing waves…

$f_{nx,ny,nz} = {v_s \over 2} \sqrt{ \left( {n_x \over L} \right)^2 + \left( {n_y \over W} \right)^2 + \left( {n_z \over H} \right)^2 }, \{ n_x, n_y, n_z = 0,1,2,3,...\}$

…both ‘forwards’ or ‘backwards’: [L,W,H] <–> [list of mode frequencies] (given speed of sound v_s).

Results

Seems to learn within +/- 5%. I don’t have a graphical representation of going from mode frequencies to room dimensions (any ideas?). For mapping dimensions to frequencies, here’s a sample room shown in the picture (red=target, green=predicted), used a training set of 200,000 random rooms. It even learns to sort the freqs in ascending order.

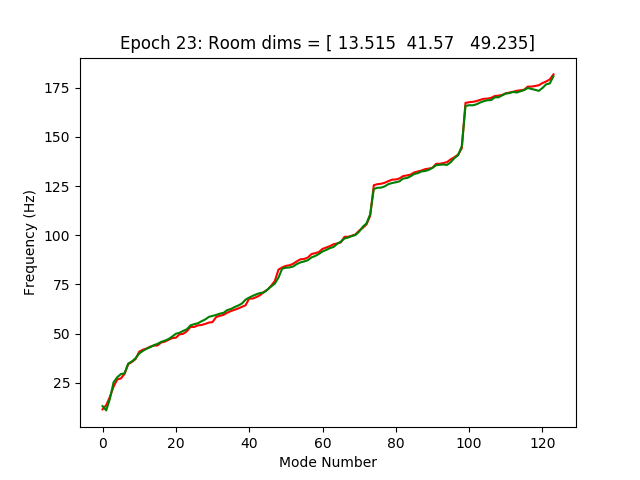
Interestingly, trying to ‘help’ the network by using squared frequencies, inverse-(squared)-dimensions, etc. actually gave worse performance than letting the network learn the nonlinearities itself. (???)

Of what possible practical utility is this? Not really sure. Although, it does a fairly decent job learning the room shape even using a smaller random subsample of the available mode frequencies. :-) If anything, it highlights a weakness of data-driven modeling: there’s no way you’ll measure 200,000 rooms in real life!

Future Work

Taking this further, would require analyzing the weights of the network in detail, to see how it represents the function approximation. Which would be worth doing!

Moving on to non-boxy rooms would be relevant and challenging. Some means of encoding the room geometry would be needed, as well some way of simulating (or measuring?) resonant frequencies or impulse responses.